What do digits, logarithms, physicists, and fraud have in common?
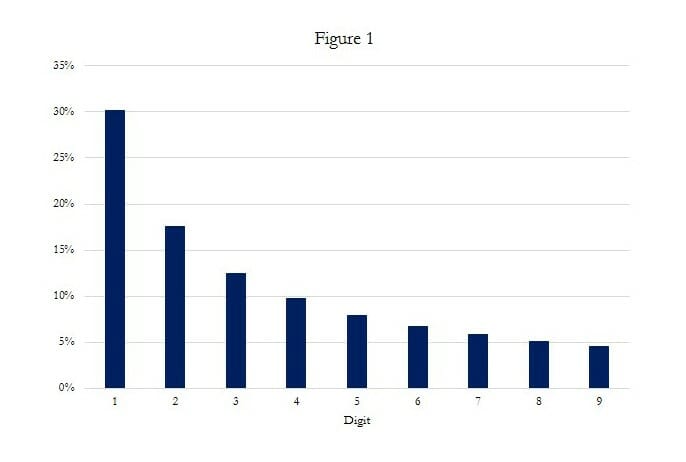
A man by the name of Frank Benford. In the 1930s, physicist Benford developed a theory of leading digits, now known as Benford’s Law. Benford’s Law tells us that in a variety of data sets, the probability of occurrence of each digit (0 through 9) as the first digit in a number follows a certain distribution. That is, the digit 1 will occur with about a 30% frequency, followed by the digit 2 at 17.6%, through the digit 9 at 4.6%. See Figure 1.
So what does this tell us, and how does it relate to fraud?
Because of its predictive component, Benford’s Law can be a useful tool for fraud examiners when applied to the right data sets – that is, large unrestricted sets of data that are not predisposed to begin with a limited number of digits. Many data analytics software programs (such as ACL, Arbutus Analyzer, and even Microsoft Excel with ActiveData) now contain a Benford function which allows users to test numerical fields in data sets for digit frequency. Leveraging this capability allows fraud examiners to quickly pinpoint (or rule out) areas for further examination and to determine anomalies and red flags for fraud, waste, and abuse.
Here’s an example of Benford at work:
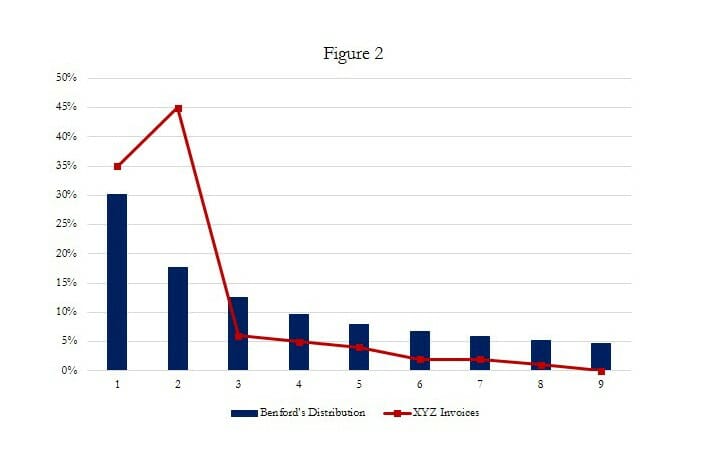
Company ABC’s purchasing policy requires that all purchases $2,500 or greater be bid out and accompanied by a purchase order. ABC employee Bill Smith is in collusion with Vendor XYZ: Smith uses ABC company funds to “purchase” hundreds of thousands of dollars’ worth of goods from Vendor XYZ and receives kickbacks from XYZ in return. Vendor XYZ submits hundreds of false invoices to ABC, each for just below ABC’s threshold of $2,500, thus circumventing ABC’s purchasing policy. ABC notices cash flow problems and hires fraud examiners to conduct a fraud vulnerability assessment. The fraud examiners run preliminary tests to identify red flags and to pinpoint areas for further examination. After running the Benford test on the purchasing data, the fraud examiners discover an anomaly in the digit distribution (see Figure 2). The fraud examiners note that the digit 2 is occurring most frequently and much more frequently than Benford’s Law would indicate that it should. The fraud examiners are then able to direct their efforts appropriately and to seek supporting documentation for the activity in question.
Add Benford to your tool kit!
Benford’s Law, which also includes second digits, first two leading digits, last digits, and other digit combinations, can be applied to credit card transactions, loan data, stock prices, transaction listings, inventory records, and much more. It is important that fraud examiners keep this tool in their kits – it may prove fruitful in future fraud examinations.